Maths education glossary: M to Z
Unsure of arrays or perplexed by partitioning? Get to know what your child is learning at school with our guide to common terms and phrases used in schools.
For help with general education terms, take a look at the Education glossary.
For help with literacy terms, take a look at the Grammar and literacy glossary.
A–L | M–Z
A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z
Mean
Mean is a kind of average. To find the mean, add up the quantities then divide by the number of quantities.
Here is how to find the mean average of 3, 3, 4, 6, and 9.
First, add the numbers together: 3 + 3 + 4 + 6 + 9 = 25
Because we added together 5 numbers, we now divide the total by 5 to find the mean: 25 ÷ 5 = 5
Therefore, the mean average of 3, 3, 4, 6, and 9 is 5.
Measurements
Units of measure: An agreed quantity by which we measure things. So, metres, centimetres, litres, millilitres, grams, and kilograms are all units of measure.
Metric measurement systems: Systems for measuring things in which the units of measure go up in 10s or multiples of 10 (100, 1000, and so on).
Kilometres, metres, centimetres and millimetres are the metric system for measuring length and distance. There are:
10 millimetres in a centimetre.
100 centimetres in a metre.
1000 metres in a kilometre.
We now use metric systems for most of our measuring.
Imperial measurement systems: Systems for measuring that were developed in England in the 19th century. Examples are pounds and ounces for measuring mass, and inches, yards and miles for measuring length and distance. We do not use them much now, except miles for measuring distance and pints for volume.
Converting between units of measure: Changing a measurement from one unit (for example, metres) to another unit (for example, centimetres). So, the measurement 2 metres can be converted to 200 centimetres.
Length and distance are measured in kilometres, metres, centimetres and millimetres. There are:
10 millimetres in a centimetre.
100 centimetres in a metre.
1000 metres in a kilometre.
Mass is measured in grams and kilograms. There are:
1000 grams in a kilogram.
Volume is sometimes measured in litres and millilitres. There are:
1000 millilitres in a litre.
Converting between imperial and metric systems of measure: It can be useful to be able to convert between common Imperial systems of measurement and the comparable metric system (for example, between miles and kilometres). To do this, you need to know the relationships between them. For instance, there are roughly:
1.6 kilometres in a mile.
0.6 miles in a kilometre.
2 pints in a litre.
0.5 litres in a pint.
Activity: Measuring length

Measure objects around your house using your handspan as a measuring tool.
Activity: Measuring mass

Weigh objects around your house and record their masses in the table.
Video: What are mass, volume and area?
Get simple definitions of mass, volume, and area and the units used to measure them.
Mental maths
The ability to calculate mentally, i.e. in your head without writing anything down. Learning things such as number bonds, number patterns, doubles, and multiplication tables facts are important mental maths skills.
Missing number problems
A calculation where one of the numbers has been taken out. The missing number could be represented by a space, question mark, or shape.
4 + ___ = 9. Children have to use related number facts to work out the answer. For instance, they may know that 9 – 4 = 5, and can therefore deduce that 4 + 5 = 9.
This type of question helps to prepare children for algebra, where unknown numbers are represented by letters.
Activity: Addition and subtraction
Drag the numbers into the boxes to complete the calculation.
Activity: Missing numbers
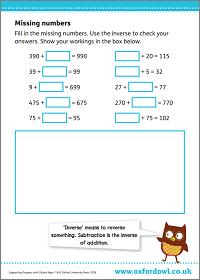
Fill in the missing numbers. Use the inverse to check your answers.
Mixed number
A mixed number is another way of showing an improper fraction, by mixing a whole number and a proper fraction.
(an improper fraction) can also be represented as 2
(a mixed number).
Non-unit fraction
A non-unit fraction is a fraction where the numerator is greater than 1.
is a non-unit fraction, because the numerator is 2.
Number
We use numbers to count quantity or to measure. Numbers have a position on a number line. There are many different kinds of number.
Video: Number bonds
Maths expert Kate Robinson explains number bonds.

Activity: Number line races
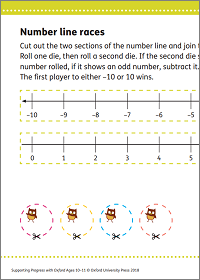
Add and subtract dice to move along number line.
Download a free number square.
Numerator
The top number of a fraction is called the numerator. The numerator tells us how many equal parts there are.
In
, the numerator is 1.
Obtuse
- An obtuse angle measures between 90° and 180°.
- An obtuse-angled triangle has one angle greater than a right angle.

Order of operations
Mathematical operations include addition, subtraction, multiplication, and division. The order of operations describes the order these should be carried out within a calculation: first anything inside brackets, then any squares or roots (orders), then any division and multiplication, and finally any addition and subtraction, working from left to right. See BODMAS.
2² × 5 + (10 – 3) = ?
We complete everything in brackets first:
2² × 5 + (10 – 3) = ?
10 – 3 = 7
2² × 5 + 7 = ?
Next, we complete any ‘order’ calculations (squares or roots):
2² × 5 + 7 = ?
2² = 2 × 2 = 4
4 × 5 + 7 = ?
Next, we complete any division or multiplication:
4 × 5 + 7 = ?
4 × 5 = 20
20 + 7 = ?
Finally, we complete any addition or subtraction:
20 + 7 = ?
20 + 7 = 27
So, 2² × 5 + (10 – 3) = 27
Activity: Addition and subtraction

Drag the numbers into the boxes to complete the calculation.
Video: What is BODMAS?
Find out the right order to solve any calculation using BODMAS.
Partitioning
Partitioning a number means to split the number into smaller chunks. It is often used to break down numbers when multiplying or dividing larger numbers to make the calculation easier.
58 × 2 can be broken down into 50 × 2 = 100 and 8 × 2 = 16, giving an answer of 116.
The grid method is one popular way of partitioning numbers.
Place value
The value of a digit depends on its place within a number. This is its place value and it is the basis of our entire number system.
In 378, there are 3 hundreds, 7 tens, and 8 ones (sometimes called units).
Activity: Place value
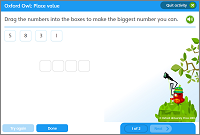
Drag the numbers into the boxes to make the biggest number you can.
Video: What is place value?
What is place value? Watch our fun animation for a simple definition.
Polygon
A polygon is any 2D shape with straight sides. Many polygons have special names. For example, triangles, squares, and rectangles are types of polygon. Polygons can be regular or irregular.
Regular polygons

Irregular polygons

Pyramid
A pyramid is a solid shape that has a polygon for a base. Each of the sides are triangles meeting at a point. The shape of the base gives the pyramid its name (e.g. a pyramid with a square base is called a square-based pyramid).


Quadrant
- A quadrant is one quarter of a circle. The straight sides of the quadrant are both radii of the circle.
- The axes of a graph divide the graph into four quadrants. In the first quadrant, both coordinates are positive. In the third quadrant, both coordinates are negative.

Quadrilateral
A quadrilateral is any polygon that has four sides. The four angles of a quadrilateral add up to 360°.

Ratio
A way of comparing the amounts of different things. For example, if a recipe asks for flour and sugar in a ratio of 2:1, it means that you need 2 lots of flour for every 1 lot of sugar that you put in.
Each thing in a ratio needs to be measured in the same kind of unit. So, if a recipe asks for flour and sugar in a ratio of 2:1 and you put in 2 cups of flour, you need to put in 1 cup of sugar. If you put in 2 kilograms of flour, you need to put in 1 kilogram of sugar. If you put in 2 bathtubs of flour, then you need to put in 1 bathtub of sugar!
You may also see ratios on map scales. In this case, it tells you the relationship between the distance on the map and the distance in real life. For example, 1:10,000 would mean that 1cm on the map represents an actual distance of 10,000cm (or 100m).
Rectangle
A rectangle is a 2D shape that has four straight sides and four right angles. The opposite sides of a rectangle are equal. A square is a special type of rectangle because all 4 sides are the same length. The word rectangle is usually used to mean the oblong rectangle.
Rectilinear
A polygon is rectilinear if it can be divided into rectangles or squares, with all the sides of the polygon meeting at right angles.
Regular
A regular polygon is any polygon with all its sides and angles the same size. A square is a regular quadrilateral.
Rhombus
A rhombus has four equal sides. The opposite sides are parallel. It is the correct name for a diamond shape.

Scale
A scale is a set of points on a line used for measuring. You can see a scale on maps, thermometers, measuring jugs, or rulers.
Sequence
A set of things (usually numbers) that are in an order. Each number in the sequence is called a term. To find missing terms in a sequence, first you need to find the rule behind the sequence. For example, in the sequence ‘2, 4, 6, 8′ the rule is to add two to the previous number. The next number in the sequence would be ’10’.
Here are some examples of sequences:
3, 6, 9, 12, 15…
The rule is to add 3 with each step.
1, 4, 9, 16, 25…
The rule is to go up in steps increasing by 2 each time (+3, +5, +7, +9, and so on).
2, 6, 18, 54, 162…
The rule is to go up by 3 times the previous number.
Shape, space, and measure
This term is used in curriculum documents and refers to work done with shapes, spatial awareness, (for example, volume, and area) and measurements (for example, centimetres, metres, and litres).
Standard unit
Standard units of measurements are units that are agreed by everyone.Metric units and imperial units are both sets of standard units.
Some standard units of length: centimetre, metre, kilometre, inch, foot, mile.
Some standard units of mass: gram, kilogram, ounce, pound.
Some standard units of capacity: millilitre, litre, pint, gallon.
Trapezium
A trapezium is a four-sided shape that has one pair of sides that are parallel. The other two sides are not parallel.

Two-step problems
A word problem that requires two steps in order to be solved is a two-step problem.
I have £6.50 to spend. If I buy two magazines priced at £1.95 each, how much money will I have left over?
This requires two steps because we need to first add £1.95 and £1.95 to each other, and then take away this total from £6.50. By going through both steps, we know that we end up with £2.60.
In later years, children will encounter multi-step problems – that is, problems involving more than two steps.
Activity: Problem solving
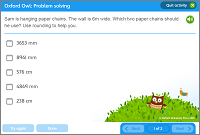
Have a go at this two-step problem.
Unit fraction
A unit fraction is a fraction which has 1 as its numerator.
is a unit fraction, because the numerator is 1.
Activity: Mystery shopper

Three word problems based on pictures of items for sale.
X-axis
The horizontal axis of a graph is called the x-axis.
Y-axis
The vertical axis of a graph is called the y-axis.