OxfordOwl

Algebra in Year 6 (age 10–11)

 

In Year 6, your child will start learning about algebra. They will use simple formulae, will describe number sequences using letters as symbols, and will find unknowns in an equation.

The key words for this section are formula, sequence, and variable.

 

What your child will learn

Take a look at the National Curriculum expectations for algebra in Year 6 (ages 10–11):

Use simple formulae

Your child will use simple formulae to solve problems. A formula is a mathematical rule that describes a relationship between quantities using symbols. For example:

The formula or  , where b stands for base and h stands for the height, finds the area of a triangle.

Generate and describe linear number sequences

A number sequence is an set of numbers ordered according to a rule. A linear number sequence increases or decreases by the same amount each time, such as 4, 8, 12, 16, 20, 24.

Your child will create linear number sequences. For example, they might be given the rule 2n + 3 and be asked to find the first five terms of this sequence. For these types of questions, it could be helpful for your child to create a table to work out the sequence:

For this sequence, the first five terms would be 5, 7, 9, 11, 13.

Your child may need to find a number in a particular position in the sequence – for example, ‘What number is tenth in the sequence?’ They should also be able to create number sequences according to a particular rule – for example, ‘Multiply by 3 and take away 1 every step’.

Express missing number problems algebraically

Your child will use letters to represent unknown numbers when solving number problems. For example:

Instead of  writing ? + 3 = 10, you child could write y + 3 = 10.

Find pairs of numbers that satisfy an equation with 2 unknown numbers

Your child will be able to find multiple solutions to equations with two unknown numbers. For example:

a + b = 8. What could a and b be?

 

The positive values for a and b could be: 7 and 1, 1 and 7, 6 and 2, 2 and 6, 5 and 3, or 3 and 5.

(As the two unknown values are represented by different letters, we will assume at this stage that a and b must be different numbers, therefore the value of a and b could not be 4 and 4.)

2a + b = 28. What could a and b be?

 

Your child will use trial and error to find different possibilities.

If they take the value of a to be 4, then 2a = 8.

So, 8 + b = 28.

Therefore, b = 28 – 8. So, b = 20.

a = 4 and b = 20 is therefore one answer to this equation.

How to help at home

There are lots of everyday ways you can help your child to understand algebra. Here are just a few ideas.

 

1. Practise basic algebra

Your child will have solved lots of problems involving missing numbers at school. Before Year 6, the unknown number in a calculation will have been represented using a blank box or a question mark. This will now be replaced by a letter, like a or b. This letter represents the unknown number, also known as the variable.

There are lots of ways you could help your child solve problems where there are one or more variables. For instance, why not play number puzzles such as the one below?

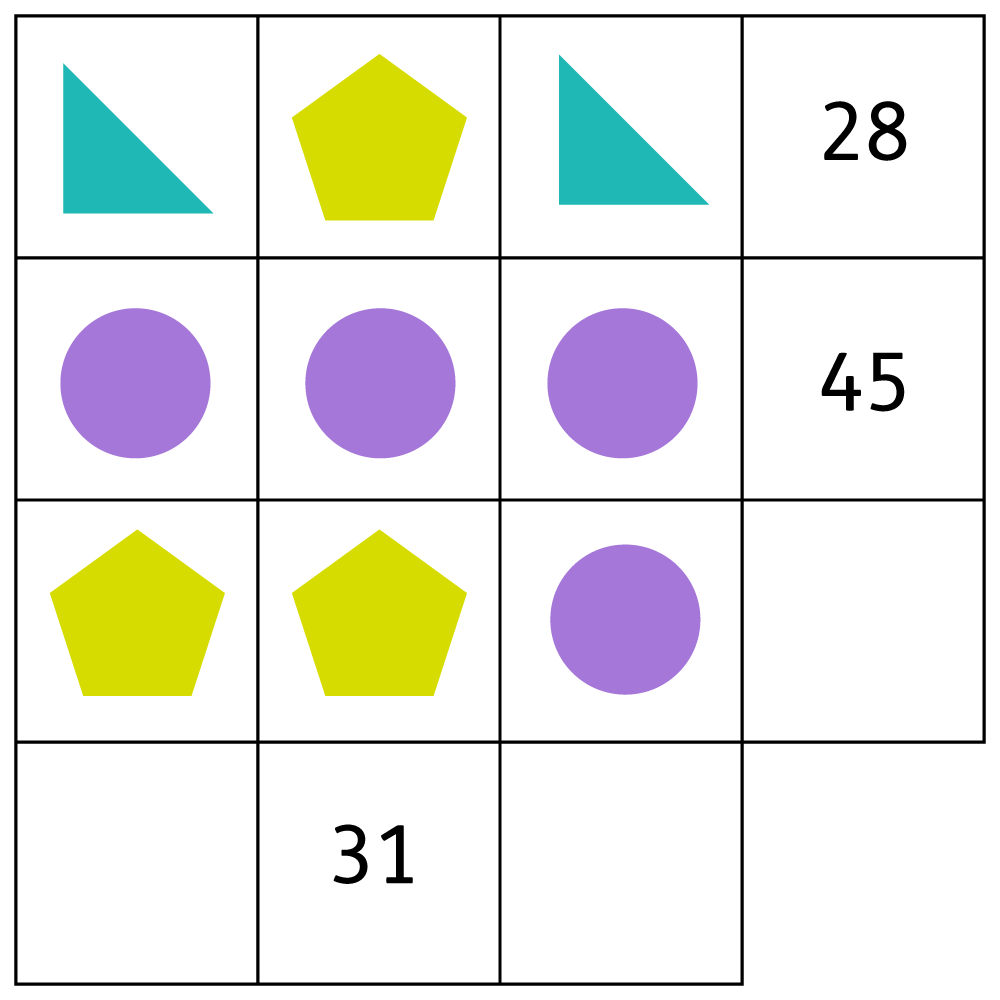
Each shape has a different value. The total value of the shapes in each column and row is shown at the end of the column or row. See if your child can work out the value of each shape and then work out the missing totals.

 

2. Play with sequences

Below are a few steps you can take to help your child get to know linear sequences:

  1. Choose a sequence of five numbers. Try to begin with sequences of numbers in the times tables. For example, start with 3 and write down the next four next terms in the sequence: 3, 6, 9, 12, 15.
  2. Can your child describe the number sequence? What is happening to the numbers in the sequence? In our example, the numbers are increasing by 3 each time, so there is a difference of 3 between each of the terms.
  3. Ask your child to predict the next few numbers. They should see that they just need to add three to get the next term. Therefore, the next two numbers in the sequence would be 18 (15 + 3) and then 21 (18 + 3).
  4. Can your child predict what the tenth number in the sequence would be? They could do this by adding on 3 ten times to reach 30.
  5. Encourage your child to look at the relationship between the position of each term (for example, the 3rd number in the sequence) and the value of that term (for example, 9). They could make a table to help them identify patterns and find a general rule:

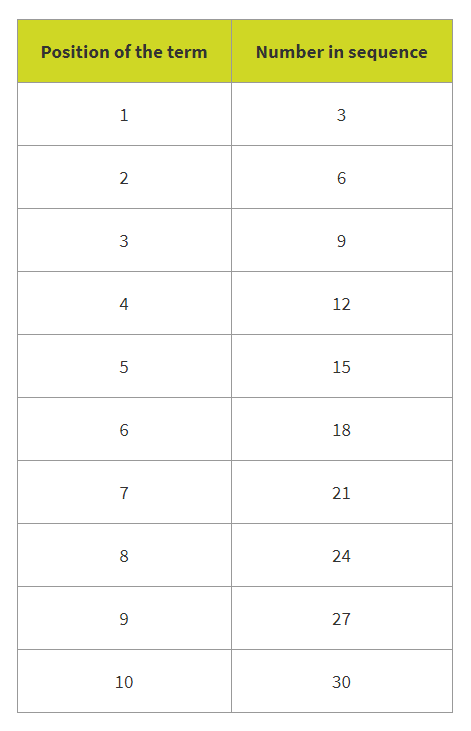
Because the number in the sequence is always the term multiplied by 3, this sequence can be written as the algebraic rule 3n.

Here are some ideas for an extra challenge once your child has followed those steps:

    • Ask your child to work out the hundredth number in the sequence. Your child should be able to see that if we multiply the term number by 3, we will get the sequence number. For example, the 100th term would be 300 because 3 × 100 = 300.
    • Ask your child if they could find any number in the sequence, like the 736th term.
    • Choose a number that you know is not in the sequence (for example, 37) and ask your child to figure out if this number would appear in the sequence. How do they know?
    • You could ask your child to explore number sequences where the numbers decrease by a constant quantity (for example, 40, 36, 32, 28, and so on).

Activity: Linear sequences

Practise your algebra skills with these questions about linear sequences.