Multiplication & division in Year 4 (age 8–9)
In Year 4, your child will learn to recall multiplication and division facts for times tables up to 12 × 12. They will use place value, number facts, factor pairs, commutativity, and inverse operations in mental calculations.
In June, your child will take part in the times tables check. Take a look at our Year 4 multiplication tables check page to find out about the assessment and to discover how you can help at home.
The key word for this section is area/grid method.
What your child will learn
Take a look at the National Curriculum expectations for multiplication and division in Year 4 (age 8–9):
Know times tables up to 12 × 12
Use place value and number facts to solve problems mentally
Your child should be able to use multiplication facts to solve division calculations and will be expected to use known facts to calculate mentally with up to three-digit numbers. For example, 600 ÷ 3 = 200 can be worked out by knowing that 2 × 3 = 6.
They will also learn to multiply three numbers together (for example, 3 × 4 × 5 = 60).
Use factor pairs and commutativity in mental calculations
They will also use their knowledge of commutativity to solve multiplication problems mentally.
Multiply two-digit and three-digit numbers by one-digit numbers
Your child will continue to practise formal written methods of multiplication and division. They will use these formal methods to solve calculations involving two-digit and three-digit numbers being multiplied by one-digit numbers (for example, 73 × 6 and 637 × 8).
They will practise the formal written method of short multiplication and short division with answers that are whole numbers.
Solve multi-step problems using rules of arithmetic
Your child will be able to write statements about the ‘equality of expressions’. This sounds complex, but it just means they can see how one way of showing a calculation has the same value as another. For example:
Using the distributive law: 39 × 7 = (30 × 7) + (9 × 7).
Using the associative law: (2 × 3) × 4 = 2 × (3 × 4).
Your child will be expected to combine their knowledge of number facts and ‘rules of arithmetic’ like BODMAS and commutativity to solve mental and written calculations (for example, 2 × 6 × 5 = 10 × 6 = 60).
How to help at home
There are lots of quick and easy ways that you can help your child to understand multiplication and division. Here are just a few ideas to support your child’s learning:
1. Find multiplication facts in real life
You can use everyday situations to practise multiplication facts. For example, if you are in the supermarket and you buy three packets of multipack crisps which have 6 packets in each, you could ask your child how many packets of crisps you will have in total. Discuss which calculation they used.
If your child knows the answer immediately, ask them what other number facts they know, if they know that 3 × 6 = 18. For example, they might know that 18 ÷ 6 = 3 or that 18 ÷ 3 = 6.
2. Use different ways of multiplying numbers
Encourage your child to use lots of methods to multiply numbers, using their understanding of:
-
- Doubling and halving. For example, if we know 2 × 6 = 12, then we also know 4 × 6 = 24, 8 × 6 = 48, and so on.
- Commutativity (i.e. knowing that we can complete multiplication sums in any order and reach the same answer). For example, if we know 2 × 6 = 12, then we also know 6 × 2 = 12.
- Inverse operations. For example, if we know 2 × 6 = 12, then we also know 12 ÷ 2 = 6 and 12 ÷ 6 = 2.
- Place value. For example, if we know 20 × 6 = 120, then we also know 200 × 6 = 1200, 2 × 0·6 = 1·2, and so on.
Encourage your child to make a mind map of all the facts they know relating to the multiplication fact 2 × 6 = 12. They might be surprised by how much they can work out from that one calculation!
The area/grid method
Your child will be taught a range of methods to solve multiplication problems at school, such as using physical resources, drawings, and diagrams such as the area/grid method. Let’s take the example 65 × 74:
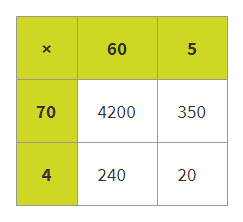
In the grid method, your child will partition (break apart) each number that is going to be multiplied. In this example, they partition each number into tens and ones – 65 is partitioned into 60 and 5, and 74 into 70 and 4. They will then find the product of each pair of numbers before adding all the values together:
70 × 60 = 4200
70 × 5 = 350
4 × 60 = 240
4 × 5 = 20
4200 + 350 + 240 + 20 = 4810
Your child will also be expected to use formal written methods like short multiplication. By practising lots of different ways of multiplying numbers, you help your child to gain confidence and flexibility in their thinking. This will let them pick the best method for any given situation.
3. Play the 1 to 21 game
You can help your child practise all four operations at home by playing the 1 to 21 game.
Ask them to roll a dice five times and record each number shown on the dice on a piece of paper. For example, 1, 4, 3, 5, 3. They then need to find a way to reach an answer of 1 using any operations (addition, subtraction, multiplication, and/or division) on the numbers.
Your child can only use each number once and they have to use at least two numbers in each calculation. For example, we could get the answer of 1 by calculating 3 ÷ 3, 5 – 4, 4 – 3, and so on. Then ask your child to find a calculation with the answer of 2 using any operation, then an answer of 3 and so on until they reach 21.
You could make this game even more challenging by saying that they have to use at least three, four, or even all five numbers to make it really tricky! Print out our activity sheet to have a go:
Activity: One to twenty-one

Find ways to make all the numbers 1 to 21.
4. Talk about factors and multiples
Try to help your child identify these and use these words when they talk about multiplication and division:
-
- Factors – a whole number that can be multiplied by another whole number to make a particular third whole number. For example, 1, 2, 3, 6, 9, and 18 are all factors of 18.
- Factor pairs – these are pairs of numbers that make up other numbers when multiplied together. For example, 6 and 3 are a factor pair of 18. Another factor pair of 18 is 9 and 2.
- Common factors – Common factors are the factors that are common to two numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 8 are 1, 2, 4, and 8. So, the common factors of 12 and 8 are 1, 2, and 4.