Ratio & proportion
As children get to the end of Primary School, ratio and proportion appear in the national curriculum. Although this is a new subject to cover, it will build on the skills and knowledge they already have.
In Year 6 your child will find missing values using ratios and solve problems involving percentages, pie charts, multiplication, and division.
-
- Ratio tells us how much of one thing there is in relation to another thing. For example, ‘For every 2 apples we have 3 bananas’.
- Proportion tells us about how much of one thing there is in relation to the whole amount of something. For example, ‘There are 50 pieces of fruit, and 1 in every 5 of those is an apple.’
How to help your child at home
There are lots of ways you can help your child to understand ratio and proportion. Here are just a few ideas:
1. Explore ratio
The concept of ratio is used in many daily activities such as cooking, using maps, or reading scale drawings. It can be very helpful to talk to your child about where and why we use ratio in our daily lives. For example:
A flapjack recipe requires 240g of oats. This makes 18 flapjacks. What quantity of oats is needed to make 24 flapjacks?
The ratio 240:18 can be established, and used to come to the answer 320g.
These types of problems will provide the foundation for formal approaches to ratio and proportion they will come across later – and you are bound to keep your child interested in ratios if you use them to make flapjacks!
2. Find percentages in real life
There are percentages to explore everywhere in the real world. For example, what percentage of your child’s class are girls? If there is 25% off the cost of something at the shops, how much money are you saving? Can you then subtract this to find out the new price?
Your child could do a survey with friends and family. For example, they could ask everyone what their favourite food is and then work out the percentage of people that chose each type of food.
3. Play the matching card game
Create some simple cards showing problems such as 15% of 300, then write the solutions to the problems on different cards. Use the cards to play pairs or snap, or just challenge your child to find the correct answer to each problem from the answer pile.
If your child has siblings, adding a bit of healthy competition to this game could help them get flying in no time!
4. Get creative
This fun salt dough craft activity is a fun way to make decorations or ornaments and practise measuring and using ratios while you are at it.
And finally, don’t worry if you are not sure how to calculate with ratios – take a look at the examples from earlier on this page or read up on ratios in our education glossary for more advice.
Want more?
To help your child’s learning further, you may want to watch some of the videos included within our dedicated maths library. If you’re looking for more ideas to support learning at home, head over to our maths blog to explore articles full of top tips and fun activities.
What your child will learn at school
For more information about your child’s learning in a particular year group, use this handy drop down menu:
Solve ratio problems involving missing values
Your child will solve ratio problems using their knowledge of multiplication and division. They will find missing values using information about the relative size of two quantities. For example:
In a survey, the ratio of the number of people who prefer milk chocolate to those who prefer white chocolate was 5:3. 46 more people prefer milk chocolate than prefer white chocolate. How many people were in the survey?
The ratio 5:3 tells us that for every 5 people who prefer milk chocolate, there were 3 who prefer white chocolate. This means that there are 2 more people who prefer milk chocolate than prefer white chocolate for every 8 people surveyed.
As there are 46 more people who prefer milk chocolate, and that number increases by 2 for every 8 people surveyed, we can work out that 23 groups of 8 must have been surveyed (46 ÷ 2 = 23). And 23 groups of 8 is 184 (23 × 8 = 184). There were therefore 184 people in the survey.
Solve problems involving the calculation of percentages
Your child will use fractions, division, and multiplication to calculate percentages. For example:
Find 15% of 360.
We can do this by first finding 10% of 360, which is 36.
Then we can find 5% of 360, which is 18.
We can then add these figures together to calculate that 15% of 360 = 36 + 18 = 54.
Alternatively, we could realise that finding 15% of a quantity is the same as multiplying by 0.15. Therefore, 360 × 0.15 gives us the answer of 54.
Your child will also be expected to solve percentage problems like this:
In Year 1 there are 50 pupils. 16 are boys and the rest are girls. What percentage of the pupils are girls?
If 16 out of 50 pupils are boys, we can convert this to a fraction with a denominator of 100:
. Therefore, 32% of pupils are boys and that means that the remaining 68% must be girls.
They will also use percentages to make comparisons. For example, they might be asked if 20% of 100 is larger than 50% of 30, and they will need to justify their reasoning.
Finally, your child will use the fact that the number of degrees in a circle is 360° to calculate percentages from pie charts. For example, they may be given the following pie chart which shows the ingredients needed to make a breakfast cereal.

They may then be asked to estimate the percentage of the mixture that is sultanas, for instance.
Solve problems involving shapes and a scale factor
Your child will solve problems involving ‘similar shapes’. These are shapes with the same proportions that are not necessarily in the same orientation or the same size. For example:
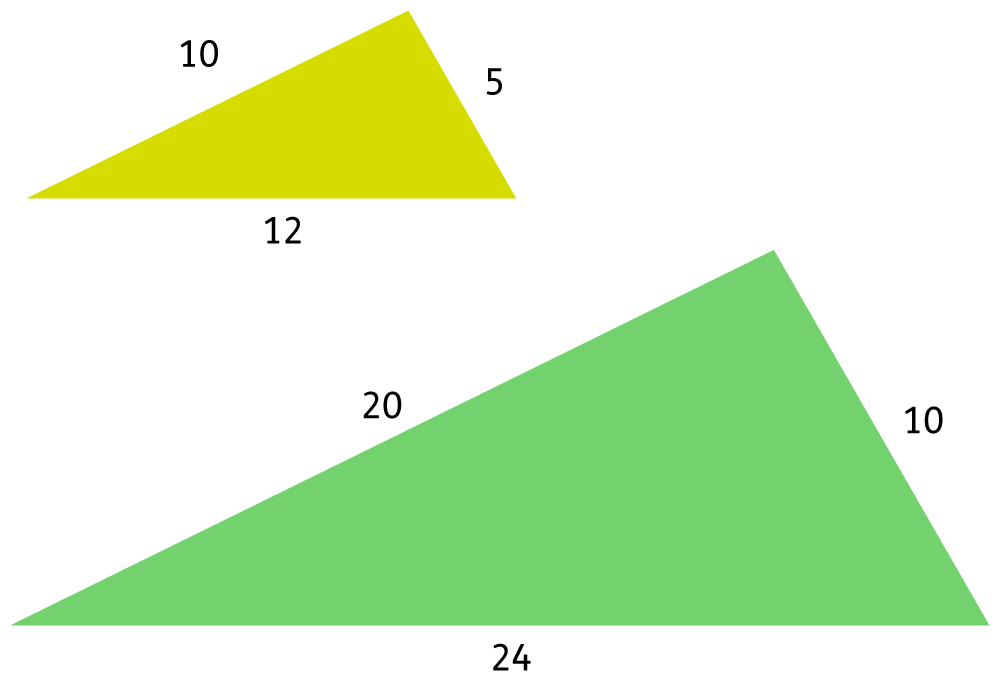
In this instance, your child might only be given the value of one of the sides of the larger shape. They may then be asked to figure out the value of the other two sides.
Your child will be expected to solve problems where the scale factor between two shapes is known or can be found. Scale factor means the amount by which you increase the size of the shape. For example, in the picture above there is a scale factor of 2, which you can work out by comparing the lengths of the sides.
Solve ratio problems involving unequal sharing and grouping
Your child will use their knowledge of fractions, division, and multiplication to solve unequal sharing or grouping problems. They may be asked to solve problems such as:
Lisa and Stephanie share £360. Lisa gets £40 more than Stephanie. How much does Stephanie get?
One way to solve this is to halve £360 to get £180, halve £40 to get £20, and then add them together to get Lisa’s cut of the money, £200. This leaves Stephanie with £160.
Your child will now be expected to express remainders as fractions and decimals. For example, in previous years children will have expressed the solution to 27 ÷ 5 as 5 remainder 2. Children will now be expected to express this remainder as a fraction (5 ) or decimal (5.4).
Find possibile combinations of two variables in an equation
Your child will be able to find numerical solutions to equations where two of the values are unknown.
For example, your child should be able to find the values of a and b that make this equation correct: 2a + b = 28. Children will use trial and error to explore different possibilities:
In the equation 2a + b = 28, you may take the value of a to be 4.
If a = 4, then 2a = 8.
So, 8 + b = 28.
Therefore, b = 28 – 8. So, b = 20.
