Fractions in Year 6 (age 10–11)
In Year 6, your child will solve lots of problems involving fractions, decimals, and percentages. They will simplify fractions using common factors and will practise multiplying fractions.
The key words for this section are common factor, numerator, denominator, improper fraction, and mixed number.
What your child will learn
Take a look at the National Curriculum expectations for fractions in Year 6 (ages 10–11):
Use common factors to simplify fractions
Your child will simplify fractions using their knowledge of common factors. For example, can be simplified to
because 4 is a factor of both 8 and 12.
Compare and order fractions
Your child will compare fractions and put them in size order.
They will be able to do this with proper fractions (i.e. fractions less than one) and fractions that are greater than one (i.e. improper fractions or mixed numbers). For example:
is greater than
is greater than
Calculate with mixed numbers and fractions with different denominators
Your child will learn to add and subtract fractions with different denominators (bottom numbers). They will do this by finding equivalent fractions that have the same denominator. For example:
+
=
+
=
Your child will also add and subtract mixed numbers. A mixed number is a number written as a whole number and a fraction (for example, 1 ).
They will use objects, diagrams, and symbols to solve problems with mixed numbers and fractions, and to explain how they have solved a problem.
Multiply and simplify proper fractions
Your child will be able to multiply pairs of proper fractions (i.e. fractions smaller than 1) together, and then write the answer in its simplest form.
×
=
=
Your child will use objects, diagrams, and symbols in their calculations.
Divide proper fractions by whole numbers
Proper fractions are fractions with a value of less than 1. Your child will be able to divide these kinds of fractions by whole numbers. For example:
÷ 2 =
Your child will do this using objects, diagrams, and symbols.
Understand the link between fractions, division, and decimals
To find
of 36cm, you would divide 36 by 4 (36cm ÷ 4 = 9 cm).
If you know
of an unknown length is 36cm and you want to find the whole length, you would multiply 36 by 4 (36cm × 4 = 144cm).
Your child will try converting simple fractions to decimal numbers (for example, = 0.375). They will know that some simple fractions have what are called ‘recurring decimal equivalents’. For example,
has a recurring decimal value of 0.333… This means it has digits that repeat forever.
Your child will also learn how to round decimals to 3 decimal places.
Use numbers with 3 decimal places
Your child will understand the value of each digit in numbers with 3 decimal places. They will also be able to multiply and divide numbers by 10, 100, and 1000, giving answers up to 3 decimal places. For example:
9 ÷ 1000 = 0.009
0·734 × 100 = 73.4
Your child will divide decimal numbers by 1-digit whole numbers. At first, they will learn this in practical contexts involving measures and money (for example, 0.65m ÷ 5 = 0.13m).
Multiply numbers with decimal places
Your child will learn to multiply 1-digit numbers with up to 2 decimal places by whole numbers. For example:
2.75 × 2 = 5.5
They will start with simple examples, such as 0.4 × 2 = 0.8, in practical contexts such as using money.
Use written division methods where appropriate
Your child will use written division methods (like long division and short division) in cases where the answer has up to 2 decimal places. You can find out more about these methods on our YouTube channel: see How to do long division and How to do short division.
Round numbers to estimate answers
Your child will round numbers and estimate answers to check their answers to decimal calculations. For example:
2.56 × 5.3 ≈ 2.5 × 5 = 12.5
So, when your child works out the question exactly, they will expect their result to be roughly 12.5. If they get an answer like 1350, they will know something has gone wrong!
Use equivalences between simple fractions, decimals, and percentages
Your child will use the connection between simple fractions, decimals, and percentages to solve problems. For example, they might remember and use the fact that = 0.5 = 50% to solve problems.
How to help at home
There are lots of ways you can help your child to understand fractions. Here are just a few ideas.
1. Help your child calculate with fractions
In Year 6, your child will continue to add and subtract fractions. They will now calculate with fractions whose denominators are the same (for example, +
), and fractions whose denominators are multiples of the same numbers (for example,
+
). They will now also be expected to add and subtract using mixed numbers (for example, 2
).
Your child might solve problems, like 3 + 2
, in the following ways.
Option 1
They could separate the whole numbers and the fractional parts:
First, add the whole numbers: 3 + 2 = 5.
Then, add the fractional parts:
+
=
.
Finally, add the whole number and fractional parts together to create a mixed number: 5
.
Option 2
They could turn each mixed number into an improper fraction, then add the improper fractions together, and finally convert the answer back into a mixed number:
First, convert 3
into an improper fraction:
.
Then, convert 2
into an improper fraction:
.
Then, add the improper fractions together:
+
=
.
Finally, turn the answer back into a mixed number:
= 5
.
The same strategies can be applied to subtracting fractions using mixed numbers.
2. Multiply and divide with fractions
Your child will multiply pairs of simple fractions – for example, ×
=
. They could be introduced to the idea using diagrams like this:
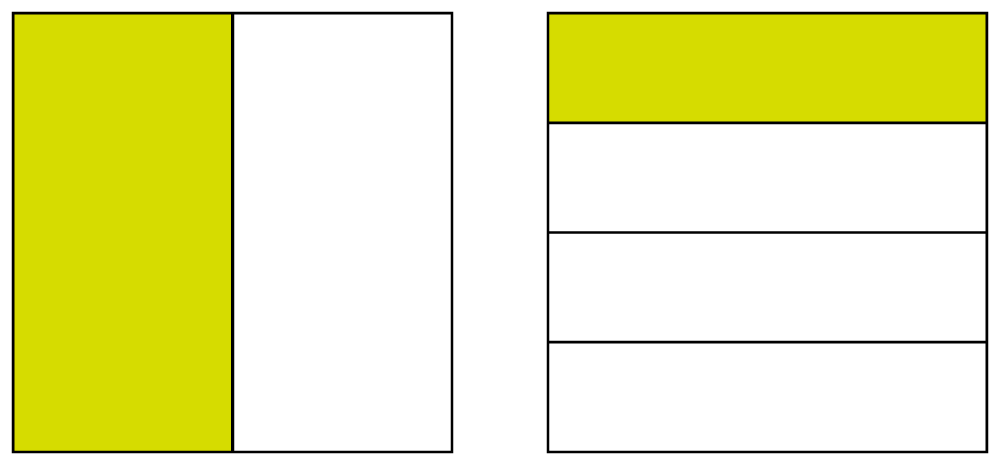
In this example, the half is shown on the left by splitting the shape vertically into two equal pieces. The same shape will then be drawn to represent quarters, this time split horizontally into four equal pieces. The diagrams will then be added together to divide the shape into eighths:

The answer can be found where the half and the quarter overlap to make one eighth:

Your child will be able to see that one out of the eight has been shaded, therefore the answer to ×
is
. Ask your child about what happens when you multiply simple fractions. You could talk about the fact that when we multiply fractions, we can multiply the two numerators and multiply the two denominators.
Your child will also learn to divide proper fractions by whole numbers – for example, ÷ 2 =
. Encourage your child to use diagrams to help them. In this example, your child could draw something to represent
and then divide it by 2:

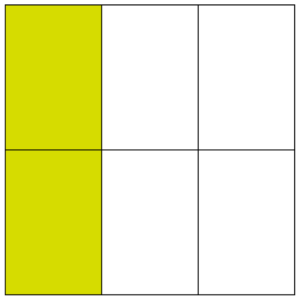

Remind your child that dividing by 2 is the same thing as finding a half of something. It might be helpful for your child to think of ÷ 2 as finding half of a third. Alternatively, they could think of the calculation as multiplying by a half. They could solve the problem by multiplying
by
. It is helpful to encourage lots of methods for calculating with fractions.
Fraction Calculations in School

Find out how your child is taught to calculate with fractions in school.
3. Calculate with decimals
Your child will continue to practise adding and subtracting with decimal numbers up to 3 decimal places. They will have to understand the effect of multiplying and dividing decimal numbers by 10, 100, 1000, and so on.
Place value charts are a great way to visualise these changes:

Help your child to understand that dividing by 10 means getting ten times smaller, dividing by 100 means getting a hundred times smaller, and so on. The same concept applies to multiplication, but the other way around.
Calculate with numbers that have 3 decimal places in the real world. For example, when you fill the car with petrol, ask your child to tell you what the number is by explaining how many tenths, hundredths, or thousandths it has. Can they round the total price or the total amount of petrol to the nearest whole number, tenth, or hundredth? For example:
If you have 56.784 litres of petrol, you could round to the nearest litre (57L), tenth (56.8L), or hundredth (56.78L).
Money and measures are great for practising using numbers with 2 decimal places. You could show your child your shopping receipt with the total hidden. Ask your child to work out the total cost of the shopping receipt. How much change you would be given if you paid using, for instance, a £10 note?
4. Link fractions, decimals, and percentages
It is important your child understands that decimals and percentages are just other ways to show fractions.
Your child will be expected to use equivalences between simple fractions, decimals, and percentages (for example, 0.5, , and 50%). To practise, encourage them to point out fractions, decimals, and percentages in real life and convert between the different forms where possible.
Fraction, Decimal, and Percentage Treasure Hunt

Practise matching percentages, decimals, and fractions on a fun treasure hunt.
5. Multiply fractions and mixed numbers by whole numbers
Your child will multiply proper fractions and mixed numbers by whole numbers.
It can often be helpful to draw diagrams when multiplying proper fractions by whole numbers, as it helps your child visualise what this means. For example, take a look at the diagram that represents multiplied by 3:

Drawings can also be a great way to support your child when they are multiplying mixed numbers by whole numbers. In the following example, 1 is multiplied by 2:
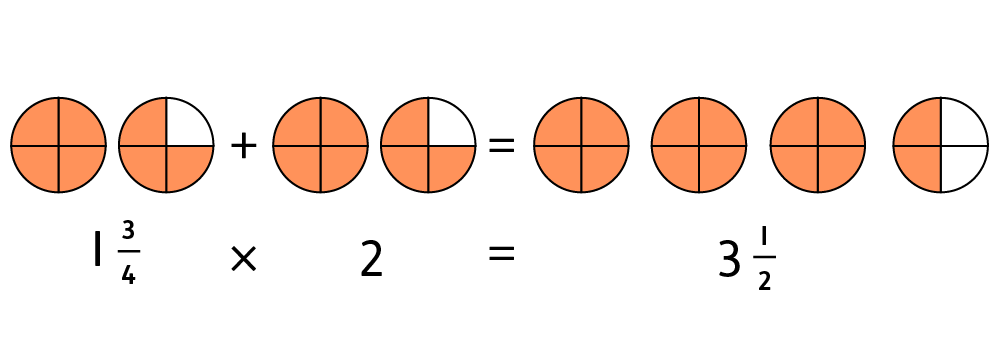
It is important to realise that × 30 =
of 30 = 30 ÷ 5. The pizza fraction cutouts in the Fraction Calculations in School booklet could be used to try out some of these calculations.
6. Percentages
Your child will continue to work with percentages. Talk about how ‘percent’ means ‘number of parts per hundred’.
Talk about numbers that are represented in percentages. For example, you could work out what proportion of your child’s class at school are girls. Ask them to tell you how to represent the percentage as a fraction and decimal (for example, 55% = = 0.55).
Sales at the shops can provide great real-life opportunities to work with percentages. For example, you could ask your child to help you work out the sale price of an item. If there is 30% off a T-shirt and the full price is £9.99, what is 30% of the full price and what is the sale price?
