Fractions in Year 5 (age 9–10)
In Year 5, your child will continue to learn about fractions as numbers, measures, and operators. They will now extend their knowledge of fractions to thousandths, and will start learning about percentages.
The key words for this section are denominator and numerator.
What your child will learn
Take a look at the National Curriculum expectations for fractions in Year 5 (ages 9–10):
Compare and order fractions
Your child will learn to compare fractions with denominators that are multiples of the same number. For example:
is less than
(also written as
<
).
The easiest way to do this is to convert both fractions into forms that have a common denominator. In this instance, we know that is equal to
. We can see that
is smaller than
, so we therefore know that
<
.
Your child will also order fractions whose denominators are all multiples of the same number. For example:
Put the fractions
,
,
,
, and
in order from least to greatest.
,
,
,
,
.
Identify equivalent fractions
Your child will learn to identify and write equivalent fractions using drawings, diagrams, and symbols. For example, children should know that is equivalent to
,
,
, and so on. Fraction walls are great for this.
In Year 5, your child will be expected to do this with fractions in the tenths () and hundredths (
).
Use mixed numbers and improper fractions
Your child will recognise mixed numbers and improper fractions, and will be able to convert one to the other.
- Mixed number: a number written as a whole number and a fraction (for example, 1
).
- Improper fraction: a fraction larger than 1 which has a bigger numerator than denominator (for example,
).
They will also be expected to convert mixed numbers to improper fractions and vice versa, for example = 1
.
Add and subtract fractions with denominators that are multiples of the same number
Your child will use drawings, diagrams, and symbols to add and subtract fractions with the same denominator, and denominators that are multiples of the same number. For example:
+
=
.
+
=
=
.
In Year 5, your child will also learn to add and subtract fractions in calculations with answers bigger than 1. To do this, they will have to use mixed numbers (for example, 1 ) and improper fractions (for example,
).
Multiply proper fractions and mixed numbers by whole numbers
Children will use objects and diagrams to:
-
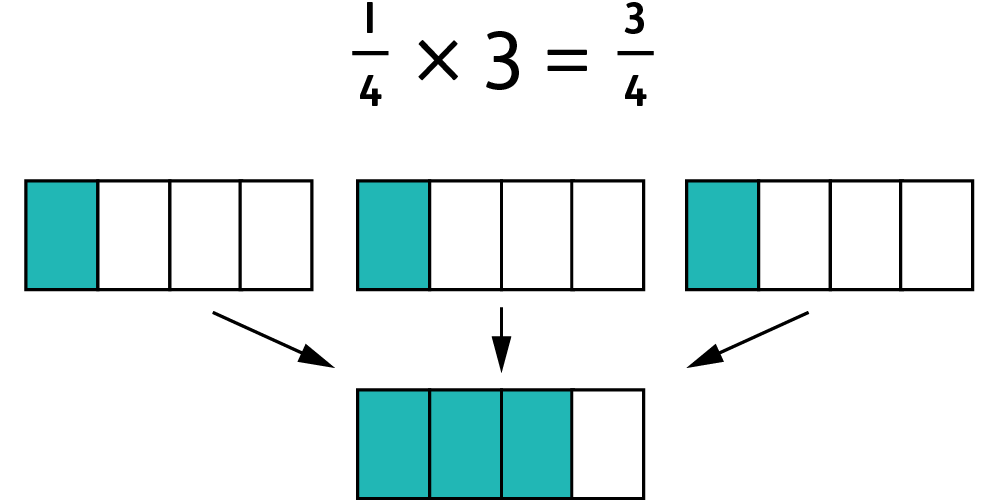
- Multiply proper fractions by whole numbers (for example,
× 3 =
).
- Multiply proper fractions by whole numbers (for example,

-
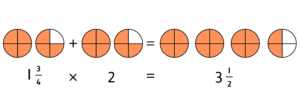
- Multiply mixed numbers by whole numbers (for example, 1
× 2 = 3
).
- Multiply mixed numbers by whole numbers (for example, 1
Read and write decimal numbers as fractions
Your child will be able to understand the equivalence between decimals and fractions. For example:
0.71 =
Use tenths, hundredth, thousandths, and their decimal equivalents
Your child will be able to say, read, and write tenths (), hundredths (
), and thousandths (
) accurately. They will also understand their decimal equivalents (for example,
= 0.29).
They will be able to mentally add and subtract tenths, as well as mixed numbers that have one-digit whole numbers and tenths.
Round numbers to one decimal place
Your child will round numbers with two decimal places up or down to the nearest whole number. For example, 3.45 will round down to 3.
They will also round numbers with two decimal places up or down to one decimal place. For example, 2.67 will round up to 2.7.
Compare numbers with three decimal places
Your child will learn to read, write, order and compare decimal numbers with up to three decimal places.
For example, they will be able to:
-
- read and write numbers with three decimal places (for example, 1.454, 1.764, 1.654, 1.453)
- put them in order (for example, 1.453, 1.454, 1.654, 1.764)
- compare them (for example, 1.453 < 3.454).
Solve problems involving numbers with three decimal places
These problems will include a mix of whole numbers and decimals, numbers with different numbers of decimal places, and complements of 1. Complements of 1 are numbers that add up to 1 (for example, 0.83 + 0.17 = 1).
Understand and use percentages
Your child will know that percentages, decimals, and fractions are different ways of expressing proportions.
They will make connections between percentages, fractions, and decimals. For example:
100% = 1
1% =
= 0·01
50% =
= 0·5
25% =
= 0·25
Your child will also recognise the percent symbol (%) and understand that ‘percent’ means ‘number of parts per hundred’. They will be able to write percentages as a fraction with denominator 100, and as a decimal fraction.
Compare percentages to fractions and decimals
Your child will know percentage and decimal equivalents of various fractions (such as ,
,
,
, and
), including fractions with a denominator of a multiple of 10 or 25. They will use this knowledge to solve problems.
How to help at home
There are lots of ways you can help your child to understand fractions. Here are just a few ideas.
1. Explore mixed numbers and improper fractions
Mixed numbers and improper fractions can be difficult for your child to grasp at first.
-
- Mixed number: a number written as a whole number and a fraction (for example, 1
).
- Improper fraction: a fraction larger than 1 which has a bigger numerator than denominator (for example,
).
- Mixed number: a number written as a whole number and a fraction (for example, 1
It often helps children to learn about these types of fractions visually. Diagrams can help their understanding:
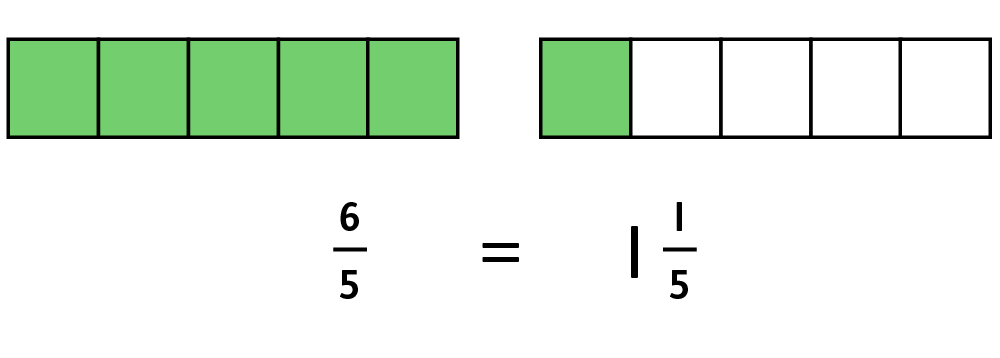
These diagrams will support your child to convert mixed numbers to improper fractions and vice versa. They can clearly see that is equivalent to 1 whole and
. You can make your own diagrams with your child using the pizza fraction cutouts in page 21 of our free Fraction Calculations in School booklet:
Fraction Calculations in School

Find out how your child is taught to calculate with fractions in school.
Ask your child to gather a number of pizza slices to make an improper fraction. Can they use these slices to show a mixed fraction? Can your child write down a mathematical way to reach the same answer?
2. Add and subtract fractions
Adding fractions
In Year 5, your child will continue to add and subtract fractions. They will now be expected to add and subtract fractions whose denominators are multiples of the same number. For example:
+
= ?
First they will need to find the lowest common denominator (i.e. the smallest multiple of the two numbers). The lowest common denominator here is 8, because it is the smallest number both 4 and 8 will divide into equally.
Your child will then have to multiply the numerator and the denominator by 2 to represent
in eighths:
Your child will now be able to add the fractions:
+
=
–
=
Subtracting fractions
Your child will follow a similar process to subtract fractions like these. For example:
–
= ?
Your child will first need to find the lowest common denominator, which is 12.
So,
will become
as the numerator and the denominator will each be multiplied by 4.
The
will become
as the numerator and the denominator will each be multiplied by 3.
Your child will then be able to subtract
from
to leave
.
–
=
–
=
More practice
You could practise calculating with fractions using the pizza cutouts in the Fraction Calculations in School booklet.
Show a calculation, such as of a pizza plus
of a pizza, to your child. Can they add the fractions by cutting and arranging the pizza slices?
For problems where the answer is greater than 1, showing how this works visually can be especially useful. For example, your child may be asked to solve +
and to record this as an improper fraction. You can show them what this means with diagrams:
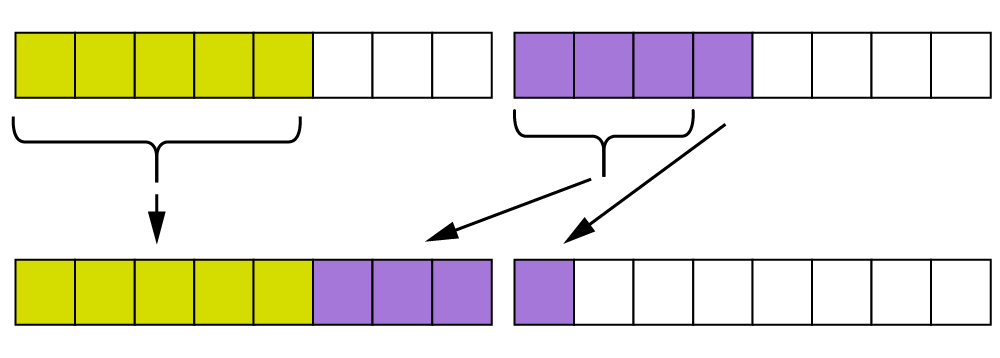
This diagram shows how +
=
, which can be recorded as an improper fraction (
) or as a mixed number (1
).
3. Multiply fractions by whole numbers
Your child will learn to multiply proper fractions and mixed numbers by whole numbers.
It can often be helpful to draw diagrams when multiplying proper fractions by whole numbers, so that your child can visualise what it means. For example, take a look at the diagram that represents multiplied by 3:
Drawings can also be a great way to support your child when they are multiplying mixed numbers by whole numbers. In the following example, 1 is multiplied by 2:

It is important to realise that × 30 =
of 30 = 30 ÷ 5. Again, the pizza fraction cutouts in the Fraction Calculations in School booklet could be used to try out some of these calculations.
4. Investigate decimals
Your child will know that decimals are another way to represent fractions (for example, is equivalent to 0·5).
Show your child a number with 3 decimal places and ask them to tell you how many tenths, hundredths, or thousandths it has. For example, the number 4·203 has two tenths, zero hundredths, and three thousandths.
Place value charts can help your child to better understand decimal numbers:

Look for examples of these numbers in the real world and point them out to your child.
For example, when filling the car with petrol, ask your child to tell you what the number is by explaining how many tenths, hundredths, or thousandths it has. You could also ask them to round the total price or the total amount of petrol up or down to the nearest whole number, tenth, or hundredth. For instance, if you used 56.784 litres of petrol, you could ask your child to round this to the nearest litre (57L), tenth (56.8L), or hundredth (56.78L).
5. Investigate percentages
In Year 5, your child will be introduced to percentages. Talk about how ‘percent’ means ‘number of parts per hundred’.
Talk about numbers that are represented in percentages. For example, you could work out what proportion of your child’s class at school are girls. Ask them to tell you how to represent the percentage as a fraction and decimal (for example, 55% = = 0.55).
Sales at the shops can provide great real-life opportunities to work with percentages. For example, you could ask your child to help you work out the sale price of an item. If there is 30% off a T-shirt and the full price is £9.99, what is 30% of the full price and what is the sale price?

